των Sobei H. Oda και Mariko Yasugi
Στο παρόν άρθρο παρουσιάζονται οι πρόσφατες προσομοιώσεις σε ηλεκτρονικό υπολογιστή και η μαθηματική μελέτη από τους συγγραφείς: υποδείγματα κυτταρικών-κυψελικών αυτομάτων (cellular automata) των μονοπωλιακών και ολιγοπωλιακών αγορών και η λογική (συντακτική) ανάλυση του «Αινίγματος των Τριών Σοφών Κοριτσιών». Δίνεται έμφαση στην ικανότητα των υποκειμένων να υπερβαίνουν το σύστημα ή, άλλως, στην ικανότητα που έχουν να σκέφτονται όχι μόνο εντός αλλά και για το σύστημα, στο οποίο τα υποκείμενα αυτά ανήκουν.
Η ανάλυση αυτής της ικανότητας, η οποία διαδραματίζει ζωτικής σημασίας ρόλο σε παίγνιο, κατά το οποίο ένας/μία παίκτης ισχυρίζεται ότι δεν γνωρίζει κάτι, θα εμβαθύνει την γνώση μας για τη διαφορά μεταξύ των ανθρώπινων κοινωνιών και των φωλιών αγριομελισσών, καθώς και για τον επιθυμητό σχεδιασμό συστημάτων ανθρώπων-μηχανών.
1. Εισαγωγή
Φανταστείτε ότι παίζουμε σκάκι. Μπορείτε να σκέφτεστε, και το ίδιο ισχύει για εμένα. Κάθε φορά που πραγματοποιείτε την κίνησή σας, πρέπει να λαμβάνετε υπόψη τί (ότι) μπορώ και εγώ να σκεφτώ. Επιπρόσθετα, πιστεύοντας ότι είμαι το ίδιο σοφός όπως και εσείς, λαμβάνετε υπόψη ότι γνωρίζω πως μπορείτε να σκέφτεστε. Τελικώς είστε σε θέση να γνωρίζετε ότι μπορώ να σκεφτώ, ότι γνωρίζω πως μπορείτε να σκεφτείτε, ότι γνωρίζω πως γνωρίζετε ότι γνωρίζω ότι σκέφτεστε,… Τέτοιες αλληλουχίες του τύπου «κάποιος γνωρίζει ότι κάποιος άλλος γνωρίζει» υπάρχουν στο μυαλό των εμπορευόμενων. Οπως σημειώνει ο Keynes (1973, p. 156) στο κεφ. 6 της Γενικής Θεωρίας, «οι επαγγελματικές επενδύσεις δύναται να παρομοιαστούν με εκείνους τους διαγωνισμούς σε εφημερίδες, στους οποίους οι διαγωνιζόμενοι πρέπει να διαλέξουν τα έξι ομορφότερα πρόσωπα μεταξύ εκατό φωτογραφιών, με το βραβείο να απονέμεται στο διαγωνιζόμενο του οποίου η επιλογή ανταποκρίνεται περισσότερο στις μέσες προτιμήσεις των διαγωνιζόμενων στο σύνολό τους.». Η σύγκριση αυτή με το διαγωνισμό ομορφιάς του Keynes, χρησιμοποιείται συχνά στην οικονομική βιβλιογραφία για την αποτύπωση της πολυπλοκότητας και της αστάθειας ενός συστήματος, το οποίο αποτελείται από υποκείμενα ικανά να σκεφτούν αλλά και δυνάμενα να γνωρίζουν ότι και οι άλλοι έχουν επίσης αυτήν την ικανότητα. Ωστόσο, ούτε ο ίδιος ο Keynes αλλά ούτε και οι νεώτεροι διάδοχοί του φαίνεται να έχουν περιγράψει ή αναλύσει πειστικά τις δυναμικές τέτοιων συστημάτων.
Επιθυμούμε να παρουσιάσουμε τις πρόσφατες προσομοιώσεις μας σε ηλεκτρονικό υπολογιστή και τη μαθηματική μελέτη που σχετίζεται με την ανάλυση ενός συστήματος που συνίσταται από υποκείμενα με δυνατότητα πραγματοποίησης λογικών συμπερασμών(1): προσομοιώσεις μονοπωλιακών και ολιγοπωλιακών αγορών, όπου οι καταναλωτές δεν λαμβάνουν υπόψη τη δυνατότητα που έχουν οι άλλοι καταναλωτές-πράκτορες(2) για πραγματοποίηση λογικών συμπερασμών (Ενότητα 2) και η ανάλυση του Αινίγματος των Τριών Σοφών Κοριτσιών (μια παραλλαγή του Αινίγματος των Τριών Σοφών Ανθρώπων του McCarthy) από την άποψη ενός καθορισμένου λογικού συστήματος (Ενότητα 3). Θα δώσουμε έμφαση στην τελευταία ανάλυση, ιδιαιτέρως δε, σε εκείνη την ικανότητα των ανθρώπων που ο Hofstadter (1979) απέδωσε τον όρο υπερβαίνοντας το σύστημα (jumping out form the system), δηλαδή στην ικανότητα να σκέφτονται όχι μόνο εντός αλλά και για το σύστημα στο οποίο ανήκουν. Στο τέλος του άρθρου (Ενότητα 4) θα συζητήσουμε για αυτήν την ικανότητα, που διαδραματίζει ζωτικής σημασίας ρόλο στο παίγνιο, κατά το οποίο ένας/μία παίκτης ισχυρίζεται ότι δεν γνωρίζει κάτι,. Ελπίζουμε επίσης ότι το παρόν άρθρο θα εμβαθύνει την γνώση μας για την διαφορά μεταξύ των ανθρώπινων κοινωνιών και των φωλιών αγριομελισσών, καθώς και για τον επιθυμητό σχεδιασμό συστημάτων ανθρώπων- μηχανών.
2. Κυψελικά Αυτόματα
2.1. Η ανάλυση των μονοπωλιακών αγορών
Ας φανταστούμε ένα ειρηνικό χωριό, όπου οι άνθρωποι πηγαίνουν για περίπατο κάθε σαββατοκύριακο. Η μοναδική έγνοια των κατοίκων αυτού του χωριού τα σαββατοκύριακα είναι το αν θα βγουν έξω στο ερχόμενο σαββατοκύριακο φορώντας ένα τριαντάφυλλο. Πέραν της τιμής των τριαντάφυλλων και της όποιας προσωπικής προτίμησης (σε κάποιους μπορεί να αρέσουν τα τριαντάφυλλα περισσότερο από ό,τι σε κάποιους άλλους), κάποιος μπορεί να λαμβάνει υπόψη του το αν αυτοί που θα βγουν το σαββατοκύριακο για περίπατο θα φοράνε τριαντάφυλλο: κάποιο άτομο μπορεί να είναι υπερ-ευχαριστημένο βλέποντας το γείτονα να φοράει τριαντάφυλλο, ενώ κάποιο άλλο μπορεί να νοιώσει απογοήτευση για αυτό.
Οι Oda et al. (1999) ανέπτυξαν ένα υπόδειγμα κυψελικών αυτομάτων για να περιγράψουν τον τρόπο με τον οποίο η συμπεριφορά-επιλογή τού να φοράει κάποιος τριαντάφυλλο, διαχέεται (μεταδίδεται) στα υπόλοιπα άτομα. Στο Σχήμα 1 απεικονίζονται τα αποτελέσματα των προσομοιώσεων για δύο παρόμοιες περιπτώσεις, κατά τις οποίες όλα τα άτομα είναι κονφορμιστές (τα άσπρα σημεία αντιπροσωπεύουν όσους φορούν τριαντάφυλλο ενώ τα μαύρα όσους δεν φορούν). Στην πραγματικότητα, από τους 10.000 κατοίκους του χωριού οι 9999 παρουσιάζουν την ίδια, για τις δύο περιπτώσεις, συμπεριφορά, κατά την αρχική χρονική στιγμή: οι 3270 φορούν τριαντάφυλλο ενώ οι υπόλοιποι 6729 όχι. Με άλλα λόγια, η μόνη διαφορά μεταξύ των δύο περιπτώσεων έγκειται στο ότι ένα άτομο, που ζει σε ένα νοτιοδυτικό μπλοκ του χωριού, φοράει στη μία περίπτωση τριαντάφυλλο ενώ στην άλλη όχι. Η μικρή αυτή διαφορά (0.1%), κατά την αρχική χρονική στιγμή, έχει ως επακόλουθο μία μεγάλη διαφορά στην τελική κατανομή της συμπεριφοράς-επιλογής των ατόμων να φορούν τριαντάφυλλο (33% έναντι 100%).
ΣΧΗΜΑ 1
2.2. Η ανάλυση των ολιγοπωλιακών αγορών
Όταν αγοράζετε μια εφαρμογή, πιθανώς λαμβάνετε υπόψη πόσο χρονικό διάστημα την έχετε χρησιμοποιήσει, καθώς και πόσοι άλλοι θα κάνουν χρήση αυτής της εφαρμογής. Ακόμα και αν είναι διαθέσιμη μια εφαρμογή υψηλότερης απόδοσης, ίσως διστάσετε να την αλλάξετε με εκείνη με την οποία είστε ήδη εξοικειωμένοι· υποψιαζόμενοι, εύλογα, ότι το να είστε σε θέση να κατέχετε πλήρως την νέα εφαρμογή απαιτεί αξιοσημείωτο χρόνο και προσπάθεια. Ίσως, ωστόσο, εγκαταλείψετε τη χρήση της αγαπημένης σας εφαρμογής, εάν ολοένα και αυξανόμενος αριθμός φίλων και συναδέλφων σας κάνουν χρήση μιας άλλης, φοβούμενοι, όχι άδικα, ότι τυχόν προσκόλληση στη δική σας εφαρμογή θα δυσχεράνει την ανταλλαγή δεδομένων και προγραμμάτων με αυτούς. Οι Oda et al. (1998) ανέπτυξαν ένα υπόδειγμα κυψελικών αυτομάτων, που περιγράφει τον ανταγωνισμό μεταξύ των δύο προϊόντων υπό αυτές τις συνθήκες, ήτοι την μέσω επαναλαμβανόμενων πράξεων διαδικασία μάθησης (learning by doing) των καταναλωτών και την δικτυακή εξωτερικότητα (network externality), οι οποίες παίζουν σημαντικό ρόλο στην αποκαλούμενη κοινωνία της πληροφορίας.
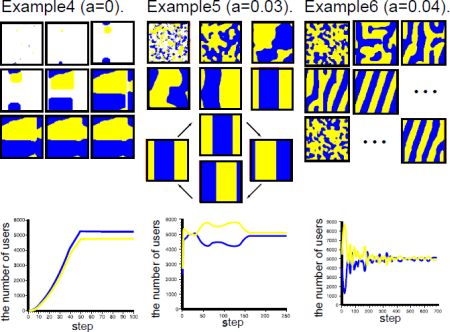
Η μακροπρόθεσμη συνέπεια του ανταγωνισμού είναι ότι, συνήθως, ο νικητής τα παίρνει όλα (Frank and Cooke 1995). Το Σχήμα 2 απεικονίζει τυπικές δυναμικές της κατανομής χρήσης μεταξύ του πρώτου προϊόντος (γκρί περιοχή) και του δεύτερου (μαύρη περιοχή). Περιπτώσεις κατά τις οποίες τα δύο προϊόντα μοιράζονται, τελικώς, την αγορά (Παράδειγμα 2) απαντώνται σπάνια. Ο λόγος είναι προφανής: το προϊόν, το οποίο κατείχε σημαντικό μερίδιο αγοράς στις προηγούμενες περιόδους, έχει πλεονεκτήματα κόστους και ζήτησης στον τρέχοντα ανταγωνισμό.
Παρόλα αυτά, πιο πολύπλοκες δυναμικές δύναται να παρατηρηθούν. Το Σχήμα 3 περιγράφει πώς αλλάζει η δυναμική της αγοράς καθώς μεταβάλλεται η παράμετρος a. Στα παραδείγματα 5 και 6 η κατανομή των χρηστών συνεχίζει να μεταβάλλεται: μία κατάσταση, η οποία δεν παρατηρείται στις προσομοιώσεις του υποδείγματος των μονοπωλιακών αγορών που αναφέρεται στην προηγούμενη υποενότητα. Αυτό υποδηλώνει ότι το υπόδειγμα της ολιγοπωλιακής αγοράς υποκρύπτει πλουσιότερες προς ανακάλυψη δυναμικές.

ΣΧΗΜΑ 2
ΣΧΗΜΑ 3
3. Συμπερασμοί εντός Γνώσης
Τα υποδείγματα κυψελικών αυτομάτων της προηγούμενης ενότητας θεωρούν τους καταναλωτές ως πράκτορες που συμπεριφέρονται σύμφωνα με ένα δεδομένο σύνολο κανόνων. Ακολουθώντας αυτό το συλλογισμό, ωστόσο, αγνοούμε μια σημαντική πλευρά-«διάσταση» της ανθρώπινης ικανότητας: ότι οι άνθρωποι μπορούν να σκεφτούν από την πλευρά ενός εξωτερικού, ως προς το σύστημα, παρατηρητή. Για να γίνει κατανοητό αυτό, ας δούμε το ακόλουθο αίνιγμα, που κατ’ουσίαν είναι το ίδιο με το Αίνιγμα των Τριών Σοφών Ανθρώπων του McCarthy(3).
3.1. Το αίνιγμα των τριών σοφών κοριτσιών
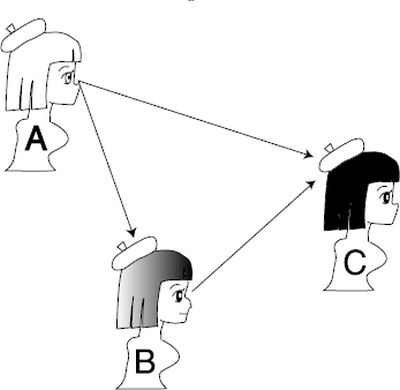
Η Άννα, η Μπιάνκα, η Κάρλα και ο Ενρίκο βρίσκοναι σε ένα θέατρο. Τα τρία κορίτσια είναι καθιστά ενώ ο Ενρίκο είναι πάνω στην εξέδρα. Κάθε κορίτσι φοράει άσπρο ή κόκκινο καπέλο, αλλά καμιά τους δεν μπορεί να δει το δικό της καπέλο στο κεφάλι της. Ωστόσο, ένα άτομο που κάθεται σε μια υψηλότερη θέση μπορεί να δει όσους/ες κάθονται σε χαμηλότερες: Η Άννα μπορεί να δει την Μπιάνκα και την Κάρλα, οι οποίες φορούν άσπρο καπέλο, ενώ η Μπιάνκα μπορεί να δει την Κάρλα, η οποία φοράει άσπρο καπέλο (βλέπε Σχήμα 4). Δεδομένων αυτών, ο Ενρίκο ρωτάει διαδοχικά τα κορίτσια:
Ενρίκο: «Άννα, εσύ, η Μπιάνκα και η Κάρλα φοράτε, η καθεμία σας, είτε άσπρο είτε κόκκινο καπέλο στο κεφάλι σας. Μπορείς να δεις αν η Μπιάνκα και η Κάρλα φορούν άσπρο ή κόκκινο καπέλο, έτσι δεν είναι;»
Άννα: «Ναι, μπορώ.»
Ενρίκο: «Μπορείς να θεωρήσεις αληθές ότι τουλάχιστον μία από τις τρεις σας φοράει άσπρο καπέλο. Μπορείς να πεις αν έχεις άσπρο ή κόκκινο καπέλο στο κεφάλι σου;»
Άννα: «Όχι δεν μπορώ.»
Ενρίκο: «Μπιάνκα, γνωρίζεις αν η Κάρλα φοράει άσπρο ή κόκκινο καπέλο. Γνωρίζεις επίσης τί γνωρίζει η Άννα και τί δεν γνωρίζει: Γνωρίζει ότι εσύ και η Κάρλα φοράτε η καθεμιά σας άσπρο ή κόκκινο καπέλο. Γνωρίζει ότι τουλάχιστον μία από εσάς φοράει άσπρο καπέλο. Δεν γνωρίζει αν η ίδια φοράει άσπρο ή κόκκινο καπέλο στο κεφάλι της. Αυτά είναι όλα όσα γνωρίζεις, σωστά;»
Μπιάνκα: «Ναι.»
Ενρίκο: «Μπορείς να θεωρήσεις ότι τουλάχιστον μία από εσένα, την Άννα και την Κάρλα φοράει άσπρο καπέλο. Μπορείς να πεις με σιγουριά αν έχεις άσπρο ή κόκκινο καπέλο;»
Μπιάνκα: «Όχι, δεν μπορώ.»
Ενρίκο: «Κάρλα, μπορείς να πεις αν έχεις άσπρο ή κόκκινο καπέλο στο κεφάλι σου;»
Κάρλα: «Ναι, μπορώ. Πρέπει να έχω άσπρο καπέλο στο κεφάλι μου.»
ΣΧΗΜΑ 4
3.2. Επιλύοντας το αίνιγμα
Μπορούμε εύκολα να μαντέψουμε πώς η Άννα, η Μπιάνκα και η Κάρλα συλλογίσθηκαν επί του αινίγματος.
Άννα: «Βλέπω ότι η Μπιάνκα και η Κάρλα φορούν άσπρο καπέλο. Είτε φοράω άσπρο καπέλο είτε όχι, τουλάχιστον δύο από εμάς φορούν άσπρο καπέλο, οπότε η δήλωση του Ενρίκο είναι αληθής. Δεν μπορώ να αποφασίσω αν το καπέλο μου είναι άσπρο ή κόκκινο»
Μπιάνκα: «Η Κάρλα φοράει άσπρο καπέλο. Εντούτοις, δεν μπορώ να συμπεράνω τίποτα για το χρώμα του δικού μου καπέλου από αυτό, διότι το μόνο που γνωρίζω είναι ότι τουλάχιστον μία από εμάς φοράει άσπρο καπέλο. Τώρα, ας εξετάσω την απάντηση της Άννας. Εάν η απάντησή της εξαρτάται από το εάν το καπέλο μου είναι άσπρο ή κόκκινο, μπορώ να πω το χρώμα του καπέλου μου. Εντούτοις, είτε το καπέλο μου είναι άσπρο είτε είναι κόκκινο, η Άννα βλέπει την Κάρλα που φοράει άσπρο καπέλο με αποτέλεσμα να μην μπορεί να πει αν η ίδια φοράει άσπρο ή κόκκινο καπέλο. Και όντως αυτό είπε. Δεν μπορώ να δω αν το καπέλο μου είναι άσπρο ή κόκκινο.»
Κάρλα: «Ας υποθέσω ότι η Μπιάνκα και εγώ φοράμε και οι δύο κόκκινα καπέλα. Τότε η Άννα μπορεί να κάνει τον εξής συλλογισμό:
«Τουλάχιστον μία από εμάς φοράει άσπρο καπέλο. Αφού ούτε η Μπιάνκα ούτε η Κάρλα φορούν άσπρο καπέλο, τότε εγώ θα πρέπει να φοράω άσπρο καπέλο στο κεφάλι μου.»
Ωστόσο, η Άννα δήλωσε πως δεν μπορούσε να πει αν φορούσε άσπρο ή κόκκινο καπέλο. Έτσι, τουλάχιστον η Μπιάνκα ή εγώ φοράμε άσπρο καπέλο.
Ας υποθέσω, τώρα, ότι το καπέλο της Μπιάνκα είναι άσπρο και το δικό μου κόκκινο. Σε αυτήν την περίπτωση η Άννα δεν μπορεί να δει αν το δικό της είναι άσπρο ή κόκκινο. Μέχρι εδώ εντάξει, αλλά η Μπιάνκα μπορεί να κάνει τον εξής συλλογισμό:
«Η Κάρλα φοράει κόκκινο καπέλο. Εάν και το δικό μου καπέλο είναι κόκκινο, η Άννα μπορεί να δει τόσο εμένα όσο και την Κάρλα να φοράμε κόκκινα καπέλα. Τότε, η Άννα, γνωρίζοντας πως τουλάχιστον ένα άτομο φοράει άσπρο καπέλο, μπορεί να αντιληφθεί πως αυτή φοράει άσπρο καπέλο. Εντούτοις, είπε πως δεν μπορεί. Άρα, το καπέλο μου πρέπει να είναι άσπρο.»
Ωστόσο, η Μπιάνκα είπε πως δεν γνώριζε αν φοράει άσπρο ή κόκκινο καπέλο. Επομένως δεν μπορεί να φοράει άσπρο καπέλο. Από αυτό συνεπάγεται ότι πρέπει να έχω άσπρο καπέλο στο κεφάλι μου.»
Είναι προφανές ότι η Κάρλα κάνουν περισσότερο πολύπλοκους λογικούς συμπερασμούς από ό,τι η Άννα και η Μπιάνκα(4). Στην πραγματικότητα, η Άννα και η Μπιάνκα κάνουν συμπερασμούς σε ανώτερο επίπεδο. Καθόσον δεν υπάρχει ουσιώδης διαφορά μεταξύ των συμπερασμών της Άννας και της Μπιάνκα, ας συγκρίνουμε τους αντίστοιχους της Μπιάνκα με της Κάρλα.
Οι συμπερασμοί της Κάρλα είναι από τους συνήθεις υπό την έννοια ότι εξάγει μηχανικά την πρόταση: «Γνωρίζω σίγουρα ότι το καπέλο μου είναι άσπρο», από αυτά που γνωρίζει σύμφωνα με κάποιους λογικούς κανόνες συμπερασμού. Στην πράξη δύναται να αποδειχθεί μέσω ενός κατάλληλα επιλεγμένου συστήματος λογικής, με τελεστές γνώσης, ότι η Κάρλα γνωρίζει πως φοράει άσπρο καπέλο (Sato, 1977).
Ωστόσο, η Άννα δεν εξάγει την πρόταση «Δεν γνωρίζω αν φοράω άσπρο ή κόκκινο καπέλο» εντός ενός λογικού συστήματος. Είναι αδύνατον, ακόμα και κάνοντας χρήση όλων των λογικών συμπερασμών εντός του συστήματος, να εξάγουμε ότι η Άννα δεν γνωρίζει αν φοράει άσπρο ή κόκκινο καπέλο από αυτά που ξέρει: Ότι, δηλαδή, η Άννα γνωρίζει πως η Μπιάνκα και η Κάρλα έχουν άσπρο καπέλο στο κεφάλι τους, και ότι τουλάχιστον μία από τις Άννα, Μπιάνκα και Κάρλα φοράει άσπρο καπέλο.
Στην πραγματικότητα, η Άννα συμπεραίνει ότι δεν γνωρίζει εάν φοράει άσπρο ή κόκκινο καπέλο εξετάζοντας το λογικό σύστημα αυτό καθαυτό. Με άλλα λόγια, η Άννα γνωρίζει ότι δεν γνωρίζει εάν φοράει άσπρο καπέλο, αποδεικνύοντας το ακόλουθο μετα-θεώρημα: «Με οποιαδήποτε επαναλαμβανόμενη εφαρμογή κανόνων εξαγωγής λογικών συμπερασμών που γνωρίζω, δεν μπορώ να αποδείξω ούτε ότι «Γνωρίζω ότι φοράω άσπρο καπέλο» ούτε την άρνηση αυτού, δηλαδή την πρόταση «Γνωρίζω ότι φοράω κόκκινο καπέλο». Είναι ένας συλλογισμός όχι εντός του λογικού συστήματος αλλά για το λογικό σύστημα.
Το αίνιγμα των τριών σοφών κοριτσιών τεκμαίρει ότι η Άννα μπορεί να βρει το μετα- θεώρημα. Πρόκειται, δηλαδή, για αποφασιστικής σημασίας εικασία ότι η Άννα δύναται να διατυπώνει συμπερασμούς τόσο εντός του συστήματος όσο και για το σύστημα. Η Άννα έχει, στην πραγματικότητα, διττό ρόλο: Η Άννα ως εντός του συστήματος και η Άννα ως παρατηρητής του, δηλ. εκτός του συστήματος. Η Άννα γνωρίζει ότι η Άννα δεν γνωρίζει εάν η Άννα φοράει άσπρο καπέλο ή όχι, αποδεικνύοντας τα ακόλουθα μετα-θεωρήματα: (i) Ότι δεν μπορεί να εξαχθεί από αυτά που η Άννα γνωρίζει, ότι η Άννα γνωρίζει πως η Άννα φοράει άσπρο καπέλο, και (ii) ότι δεν μπορεί να εξαχθεί από αυτά που η Άννα γνωρίζει, ότι η Άννα γνωρίζει πως η Άννα φοράει κόκκινο καπέλο. Με άλλα λόγια, η Άννα υπερβαίνει το σύστημα, εξετάζει το σύστημα και συμπεραίνει ότι δεν γνωρίζει αν φοράει άσπρο ή κόκκινο καπέλο. Δεν μπορεί να καταλήξει σε τέτοιου είδους συμπέρασμα, αν παραμείνει εντός του συστήματος.
Το αίνιγμα των τριών σοφών κοριτσιών αναπαριστά ένα χαρακτηριστικό που διακρίνει τον ανθρώπινο συλλογισμό: Ότι οι άνθρωποι μπορούν να υπερβαίνουν το σύστημα . Αυτό σημαίνει ότι (i) το ανθρώπινο oν δύναται να παρατηρεί το σύστημα στο οποίο ανήκει, να αποδεικνύει μετα-θεωρήματα, να ενσωματώνει αυτά στο αρχικό σύστημα, και να διατυπώνει περαιτέρω συμπερασμούς εντός του επαυξημένου, καταυτόν τον τρόπο, συστήματος, και (ii) το ανθρώπινο ον μπορεί να επαναλαμβάνει το (i) όσες φορές απαιτείται, θεωρώντας ότι και τα άλλα ανθρώπινα όντα μπορούν να το κάνουν αυτό.
Αναμφίβολα, λίγοι άνθρωποι ή, μάλλον, κανείς άλλος εκτός από τους ειδικούς της Λογικής, θα μπορούσαν να αποδείξουν αυστηρά τα προαναφερόμενα μετα-θεωρήματα μέσω τεχνικών όρων της Λογικής (Oda and Yasugi, 1999, και Yasugi and Oda, 1999). Ωστόσο, ένας μέσος μαθητής συχνά επιλύει ορθά το αίνιγμα των τριών σοφών κοριτσιών. Αυτά τα παιδιά μπορούν να υπερβαίνουν το σύστημα, και να παίρνουν ως δεδομένο ότι και η Άννα, όντας άνθρωπος, μπορεί να υπερβαίνει το σύστημα. Στα υποδείγματα προσομοίωσης, τα αυτόματα και οι πράκτορες στερούνται αυτής της ικανότητας. Ενώ είναι σε θέση να κάνουν συμπερασμούς εντός ενός δεδομένου λογικού συστήματος, είναι ανίκανα να υπερβαίνουν το σύστημα και να αποδεικνύουν μετα-θεωρήματα ώστε να επαυξάνουν την ισχύ του τρόπου συλλογισμού τους.
4. Συμπερασματικές Παρατηρήσεις
Οι θεωρίες και τα αναλυτικά εργαλεία για την κατανόηση δυναμικών συστημάτων ευρείας κλίμακας στο πεδίο της Φυσικής και της Βιολογίας είναι εφαρμόσιμα και όντως εφαρμόζονται στα οικονομικά. Τα κυψελικά μας αυτόματα αποτελούν τέτοια παραδείγματα: ένας αριθμός πρακτόρων (αυτόματα), καθένας από τους οποίους ακολουθεί ένα συμπεριφορικό κανόνα, που ορίζεται από ένα σύνολο εντολών του τύπου εάν-τότε, αλληλεπιδρούν μεταξύ τους παράγοντας τη δυναμική του όλου συστήματος. Πιστεύουμε ότι αυτή η προσέγγιση θα μπορούσε να συνδέσει την πραγματική οικονομία με τις οικονομικές θεωρίες: η πρώτη δύναται να παρατηρηθεί μόνον εν μέρει, με ορισμένα σφάλματα, ενώ οι δεύτερες είναι αυστηρά διατυπωμένες, κάτω από έναν αριθμό παραδοχών, μερικές από τις οποίες είναι μάλλον μη-ρεαλιστικές.
Ωστόσο, τα υποδείγματά μας φαίνεται πως αναπαράγουν μόνο εκείνες τις δυναμικές, οι οποίες παρατηρούνται στα υποδείγματα κυψελικών αυτομάτων που έχουν κατασκευαστεί στα πεδία των επιστημών και της μηχανικής. Ο λόγος είναι, κατά τη γνώμη μας, ότι τα δικά μας υποδείγματα αγνοούν το γεγονός ότι τα ανθρώπινα όντα δεν είναι απλοί πράκτορες που συμπεριφέρονται σύμφωνα με δεδομένους κανόνες. Στην πραγματικότητα, οι άνθρωποι μπορούν να υπερβαίνουν το σύστημα και να σκέφτονται για το σύστημα στο οποίο ανήκουν και τους κανόνες που ακολουθούν, λαμβάνοντας υπόψη ότι και οι άλλοι μπορούν επίσης να το κάνουν.
Η ανθρώπινη ικανότητα της υπέρβασης του συστήματος πρέπει να εισαχθεί καταλλήλως στην έρευνα της πολυπλοκότητας. Η πολυπλοκότητα που προσιδιάζει στις ανθρώπινες κοινωνίες, πολυπλοκότητα που γεννάται από την υπέρβαση του συστήματος από τα υποκείμενα, δεν μπορεί να αναπαραχθεί φτιάχνοντας απλώς πιο σύνθετους ή εξελιγμένους συμπεριφορικούς κανόνες για τους πράκτορες. Η Τεχνητή Κοινωνία (Epstein and Axtell, 1996) μοιάζει όχι με κοινωνία ανθρώπων αλλά εντόμων. Πιστεύουμε ότι, καίτοι απλή, η διατύπωσή μας περί υπέρβασης του συστήματος, σε όρους Δυνητικών (Τροπικών) Λογικών, μπορεί να είναι χρήσιμη για την προώθηση της έρευνας σε αυτήν την κατεύθυνση.
Τα ανθρώπινα όντα κάνουν συμπερασμούς τόσο εντός όσο και για το σύστημα. Είναι αυτή η ανθρώπινη ικανότητα που δίνει στο σύστημα, το οποίο συντίθεται από ανθρώπους, διακριτές ποιότητες. Τα ανθρώπινα όντα που δεν μπορούν να συμπεριφερθούν μηχανικά, ως μέρη του συστήματος, ενδέχεται συχνά να αποτελούν ασθενή σημεία του συστήματος, αλλά μπορούν να υπερβαίνουν το σύστημα παρατηρώντας το από έξω: Κάνοντας αυτό, μπορούν να ανταπεξέρχονται σε αναπάντεχα γεγονότα (τυχήματα) και να βελτιώνουν το σύστημα στο οποίο ανήκουν. Ορισμένα τυχήματα σίγουρα προκαλούνται από ανθρώπινα λάθη (εσφαλμένη υπέρβαση του συστήματος), αλλά κάποια άλλα αποτρέπονται ή ελαχιστοποιούνται από την ανθρώπινη επινοητικότητα (κατάλληλη υπέρβαση του συστήματος).
Στην πραγματικότητα, η υπέρβαση του συστήματος από τα ανθρώπινα όντα δεν είναι απλώς εφικτή, αλλά είναι και αδύνατον να μην λαμβάνει χώρα. Τα μυρμήγκια-εργάτες μπορεί να πηγαίνουν στη δουλειά τους χωρίς να ρωτάνε γιατί: Είναι πραγματικά αξιόπιστα μέρη της φωλιάς. Τα ανθρώπινα όντα δεν μπορούν να δουλέψουν κατ’αυτόν τον τρόπο: Δεν μπορούν παρά να βρίσκουν κάποιο νόημα στην εργασία τους, βάσει του οποίου είτε θα δουλεύουν σκληρότερα είτε θα τη σαμποτάρουν.
Πρέπει να τεθεί ένα όριο στην προσέγγιση που περιγράφει την εξέλιξη των οικονομιών ως διαδικασία αλληλεπιδράσεων μεταξύ πρακτόρων που δεν μπορούν να υπερβούν το σύστημα. Καίτοι αποτελεί σημαντικό μέρος της, η οικονομία δεν είναι όλη η κοινωνία. Εάν κάποιος αναπτύσσει τέτοιες θεωρίες, οι οποίες παίρνουν ως δεδομένο ότι κάθε πράκτορας επιδιώκει τους οικονομικούς του στόχους σε ένα δεδομένο οικονομικό σύστημα, τότε μπορεί να μην κατανοεί την πραγματική οικονομία χωρίς να ρωτάει πότε και πώς τα ανθρώπινα όντα υπερβαίνουν το οικονομικό τους σύστημα και τι επιδράσεις έχει αυτό στα άτομα, στο οικονομικό τους σύστημα καθώς και σε ολόκληρο το κοινωνικό σύστημα.
Προκειμένου να αναπαράγουμε και να αναλύσουμε την πολυπλοκότητα που είναι συνυφασμένη με το σύστημα που συντίθεται από ανθρώπινα όντα, πρέπει να συνεχίσουμε τις θεωρητικές και εμπειρικές μελέτες των λογικών συμπερασμών εντός αλλά και για το σύστημα, και να τις ενσωματώσουμε στη γενική θεωρία των σύνθετων συστημάτων. Αυτήν την περίοδο, αναπτύσσουμε θεωρητική έρευνα, λαμβάνοντας υπόψη ότι η υπέρβαση του συστήματος είναι η επιπρόσθεση γνώσης, η οποία βασίζεται στη μετα-σκέψη, σε όρους θεωρίας αποδείξεων:
Ειδικότερα, σε όρους αποδειξιμότητας (provability) και μη-ασυνέπειας (non-inconsistency). Προς το παρόν έχουμε παραστήσει μόνον αυτό που κάποιος/α γνωρίζει αληθινά όταν ισχυρίζεται ότι δεν γνωρίζει κάτι, πώς κάποιος/α μεγεθύνει το σύστημα της γνώσης του/της όταν γνωρίζει ότι κάποιος/α άλλος/η δεν γνωρίζει κάτι, κ.λπ.. Ευελπιστούμε ότι η μελέτη μας μπορεί να αναπτυχθεί περαιτέρω εισάγοντας τα αποτελέσματα της θεωρίας παιγνίων και των πειραματικών οικονομικών (experimental economics)(5). Οι θεωρίες και οι ποικίλες εφαρμογές τους θα ήταν χρήσιμες σε αυτήν την έρευνα. Ελπίζουμε ότι ερευνητές διαφόρων ειδικοτήτων θα συμμετάσχουν στο ερευνητικό μας σχέδιο.
Μετάφραση: Στέλιος Σφακιωτάκης
Επιμέλεια: Θεόδωρος Μαριόλης
Ευχαριστίες
Ευχαριστούμε τον Στέλιο Σφακιωτάκη και τον Καθηγητή Θεόδωρο Μαριόλη για τη μετάφραση και την επιμέλεια, αντιστοίχως, του άρθρου μας στην ελληνική γλώσσα, το οποίο δημοσιεύεται για πρώτη φορά, σε περιοδικό, εδώ. Η αρχική εκδοχή του, η οποία περιείχε ένα προβληματικό αριθμητικό παράδειγμα (στο Σχήμα 3), πράγμα που οφειλόταν σε σφάλμα του υπολογιστικού προγράμματος προσομοίωσης, παρουσιάστηκε στο «Διεθνές Εργαστήριο στην Αναδυόμενη (ή Αναδυτική)6 Σύνθεση» (6-7 Δεκεμβρίου 1999, Πανεπιστήμιο Κόμπε, Κόμπε, Ιαπωνία) και δημοσιεύτηκε στα Πρακτικά του (pp. 257-262), ενώ η συγγραφή της διεξήχθη στα πλαίσια του ερευνητικού προγράμματος: «Μεθοδολογία της Αναδυτικής Σύνθεσης», το οποίο υποστηρίχθηκε από την Ιαπωνική Εταιρεία για την Προώθηση της Επιστήμης (Japan Society for the Promotion of Science, JSPS-RFTF96P00702).
ΣΗΜΕΙΩΣΕΙΣ
1 Συμπερασμός: η διαδικασία εξαγωγής λογικών συμπερασμάτων από προτάσεις (premises) που είναι, ή θεωρείται ότι είναι, αληθείς. Ο αγγλικός όρος είναι: inference. (ΣτΜ)
2 Ο «πράκτορας», στην οικονομική ορολογία, έχει την έννοια του αυτόνομου δρώντος- συμμετέχοντος σε ένα υπόδειγμα απόφασης ή σε ένα κοινωνικό σύνολο. Στην τεχνητή νοημοσύνη, ο «ευφυής πράκτορας» (intelligent agent) είναι μια αυτόνομη οντότητα που δύναται να αντιλαμβάνεται, μέσω αισθητήρων, το περιβάλλον και να αντεπιδρά, μέσω ενσωματωμένων ενεργοποιητών (actuator), πάνω σε αυτό, με σκοπό την επίτευξη συγκεκριμένων στόχων. Ένας θερμοστάτης, για παράδειγμα, αποτελεί «ευφυή πράκτορα», σύμφωνα με τα παραπάνω. (ΣτΜ)
3 Στην ελληνική βιβλιογραφία εντοπίζουμε μία ενδιαφέρουσα, παιδαγωγική εισαγωγή στη «Φιλοσοφία της Γλώσσας» μέσω μίας παραλλαγής αυτού του αινίγματος: Βώρος, Φ. Κ. (1982) Δοκίμια Φιλοσοφίας, Αθήνα, Σ.Ε.Λ.Μ.Ε., σσ. 69-85 (Σ.τ.Ε.)
4 Η όλη διεργασία επίλυσης και οι συμπερασμοί του συγκεκριμένου αινίγματος έχουν διατυπωθεί και φορμαλιστικά από τους ίδιους συγγραφείς στο Oda and Yasugi (1999, pp. 4-6) (ΣτΜ) Υπερβαίνοντας το σύστημα 160 Μαρξιστική επιθεώρηση PRAXIS
5 Όπως το διατύπωσε ο ίδιος, στο περιθώριο του «Εργαστηρίου στην Πολιτική Οικονομία», Τμήμα Δημόσιας Διοίκησης, Πάντειο Πανεπιστήμιο, 29 Μαρτίου 2007, ο Καθηγητής Oda στράφηκε, στα τέλη της δεκαετίας του 1990, στον κλάδο των «πειραματικών οικονομικών», όταν επιχείρησε να μελετήσει, κατανάγκην μέσω προσομοιώσεων σε υπολογιστή, μη αναλογικώς μεγεθυνόμενα καθέτως ολοκληρωμένα συστήματα à la Pasinetti (σχετικά, βλ. Oda, S. H. (2007) Formulating non-proportionally growing economies: a generalisation of Pasinetti’s analysis, Bulletin of Political Economy, 1, pp. 129-159). Για ένα αντιπροσωπευτικό δείγμα του έργου του, και του έργου άλλων, σε αυτόν τον κλάδο, βλ. Oda, S. H. (Ed.) (2007) Developments on Experimental Economics. New
Approaches to Solving Real-World Problems, Berlin, Springer. (Σ.τ.Ε.)
6 Για την έννοια της «αναδυτικότητας», στη Γενική Θεωρία των Συστημάτων, βλ. Willke, H. (1996) Εισαγωγή στη Συστημική Θεωρία, Αθήνα, Κριτική, κεφ. 5. (Σ.τ.Ε.)
ΑΝΑΦΟΡΕΣ
Epstein, J. M. and Axtell, R. (1996) Growing Artificial Societies, Cambridge MA, MIT Press.
Frank, R. H. and Cook, T. P. J. (1995) The Winner-Take-All Society. Why the Few at the Top Get So Much More Than the Rest of Us, New York, Free Press.
Hofstadter, D. R. (1979). Gödel, Escher, Bach, New York, Basic Books.
Keynes, J. M. (1973) The General Theory of Employment, Interest and Money, in: The collected writings of John Maynard Keynes, Vol. 7, London, Macmillan.
Oda, S. H., Iyori, K., Miura, K, and Ueda, K. (1998) The application of Cellular Automata to the Consumer’s Theory: Simulating the Diffusion of Rivaling Products, Lecture Notes in Artificial Intelligence 1585: Simulated Evolution and Learning, edited by B. McKay et al., Berlin,Springer.
Oda, S. H. and Yasugi, M. (1999) Inference within knowledge, presented at the Annual Conference of the Japan Association of Economics, University of Tokyo, 16-17 October, 1999 [δημοσιεύτηκεως: Yasugi, Μ. and Oda, S. H. (2003) Notes on bounded rationality, Scientiae Mathematicae Japonicae, 57, pp. 83-92].
Oda, S. H., Miura, K., Ueda and Baba, Y. (1999) The application of cellular automata and agent model to markets with network externalities, in: Commerce, Complexity and Evolution, Vol. 11 of International Symposia in Economic Theory and Econometrics, edited by W. Barnetti, C.
Chiarella, S. Keen, R. Markus and H. Schnabl, Cambridge, Cambridge University Press.
Sato, M. (1977) A study of Kripke-type Models for Some Modal Logics by Gentzen’s Sequential Method, Publications of RIMS, Vol. 13, pp. 381-468, Research Institute of Mathematical Sciences, Kyoto University, Kyoto, Japan.
Yasugi, M. and Oda, S. H. (1999) A Proof-theoretic approach to knowledge, to appear in the Proceedings of the seventh Asian Logic Conference (Hsi-Tou, Chinese Taipei, 6-10 June, 1999) [άλληεκδοχήδημοσιεύτηκεως: Yasugi, Μ. and Oda, S. H. (2002) A Note on the wise girls puzzle, Economic Theory, 19, pp. 145-156].

